Quelle est la différence entre matriciel et vectoriel ?

Quelle est la différence entre matriciel et vectoriel ?

Le numérique est un champ de bataille où s’affrontent deux types d’images distinctes : les images matricielles et les images vectorielles. Comprendre la distinction entre celles-ci est fondamental pour s’en servir à bon escient. Le but de cette page est d’éclaircir cette distinction.

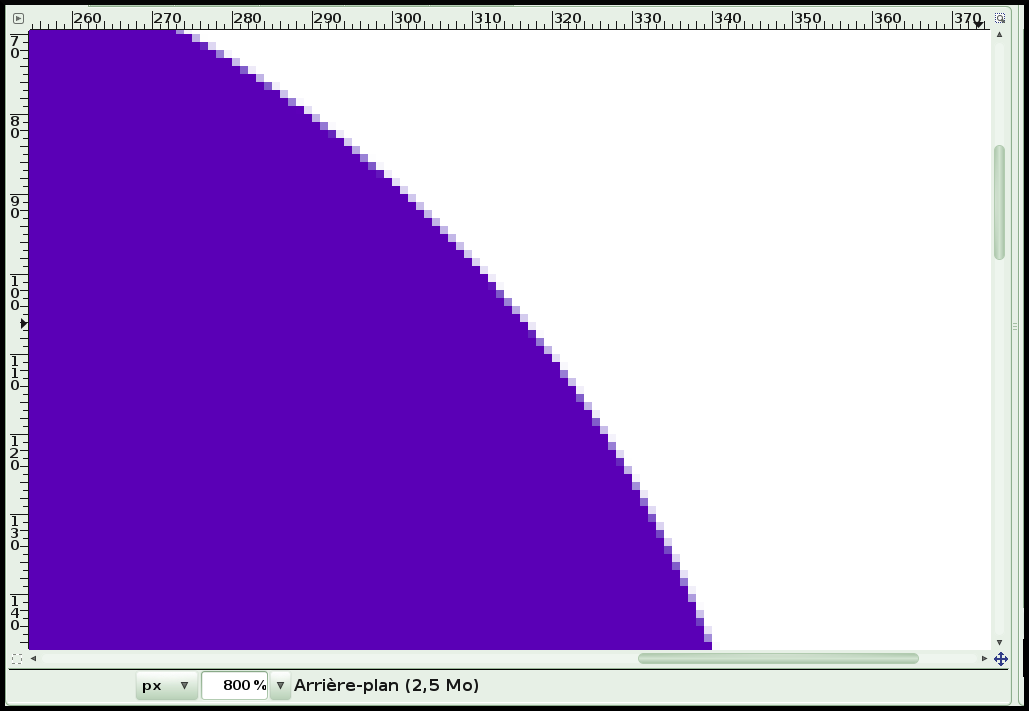
Pour commencer, voici un cercle que j'ai dessiné dans le logiciel GIMP, qui traite des images matricielles :

Jusqu’ici, tout va bien. Je décide alors de zoomer sur le bord de mon cercle, en maintenant Ctrl et en utilisant la molette de la souris vers le haut. Stupeur ! Que vois-je apparaître !?

La jolie courbe de mon cercle est maintenant toute rugueuse… Vous le savez, ce que nous voyons là sont des pixels !

Qu’est ce qu’un pixel ? C’est le composant fondamental de l’écran de l’ordinateur.

Le nombre de pixels présent à l'écran s'appelle la résolution de l’écran : la résolution standard d’un écran est aujourd’hui 1920 x 1080, c’est-à-dire qu’il est constitué de 1920 colonnes de 1080 pixels, soit 2 073 600 pixels !

Chaque pixel est lui-même constitué de 3 LEDs : une rouge, une verte et une bleue, dont la balance permet de reconstituer toutes les couleurs que peut percevoir l’œil humain.

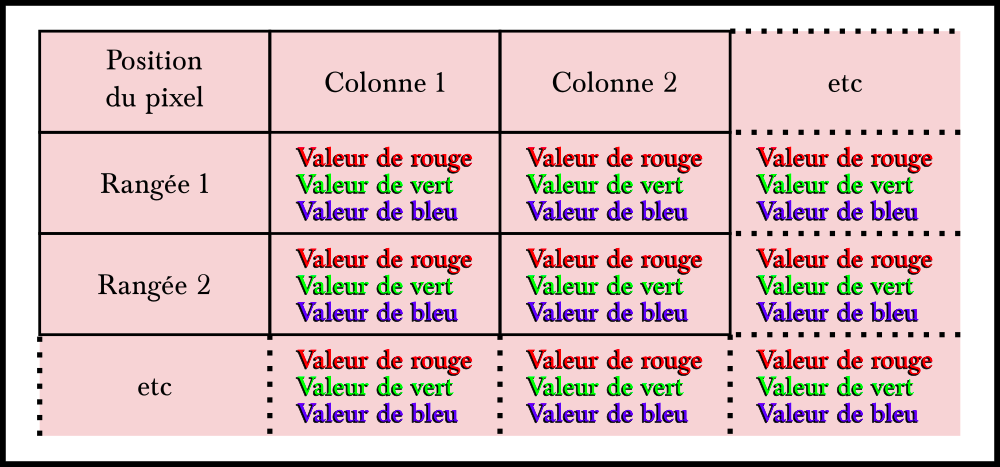
Pour pouvoir afficher une image à l’écran, nous avons en fait besoin d’un tableau en deux dimensions qui ressemble à ceci :

C’est de cette manière que l’appareil photo fonctionne. À partir des informations lumineuses que son capteur reçoit, celui-ci crée un tableau de valeurs de luminosité qu’on appelle communément une photo numérique. Cette représentation correspond au
format de fichier nommé JPEG. Le format PNG est similaire dans son mode de fonctionnement mais ajoute une quatrième valeur au pixel : sa transparence.

Voici une image prise à l’appareil photo dont j’ai extrait un carré de 25 x 25 pixels, puis que j’ai agrandi :

Les colonnes et rangées sont bien visibles. Il y en a 25 de chaque. Chaque carré contient trois valeurs de couleurs, une pour le rouge, une pour le vert et une pour le bleu.

Un problème se pose avec cette méthode : du fait que cette manière de stocker les données possède une taille minimale : il n’est pas possible de zoomer à l’infini. À un zoom de 100%, c’est-à-dire à taille réelle, à chaque pixel de l’écran correspond un pixel du fichier.
Cependant, à un zoom de 200%, un pixel du fichier correspond à 4 pixels de l’écran (en forme de carré). Ces 4 pixels ont donc la même couleur, puisqu’il n’y a pas d’information de couleur plus petite. L’image est pixelisée.

 

De ce fait, on peut déduire que lorsque l’on travaille avec une image matricielle, il ne faut jamais augmenter son zoom au-delà de 100%. C’est à partir de cette limite que l’image sera pixelisée. Il vaut mieux avoir en tête la résolution maximale qu’aura
l’image et générer le fichier en fonction de ce paramètre.

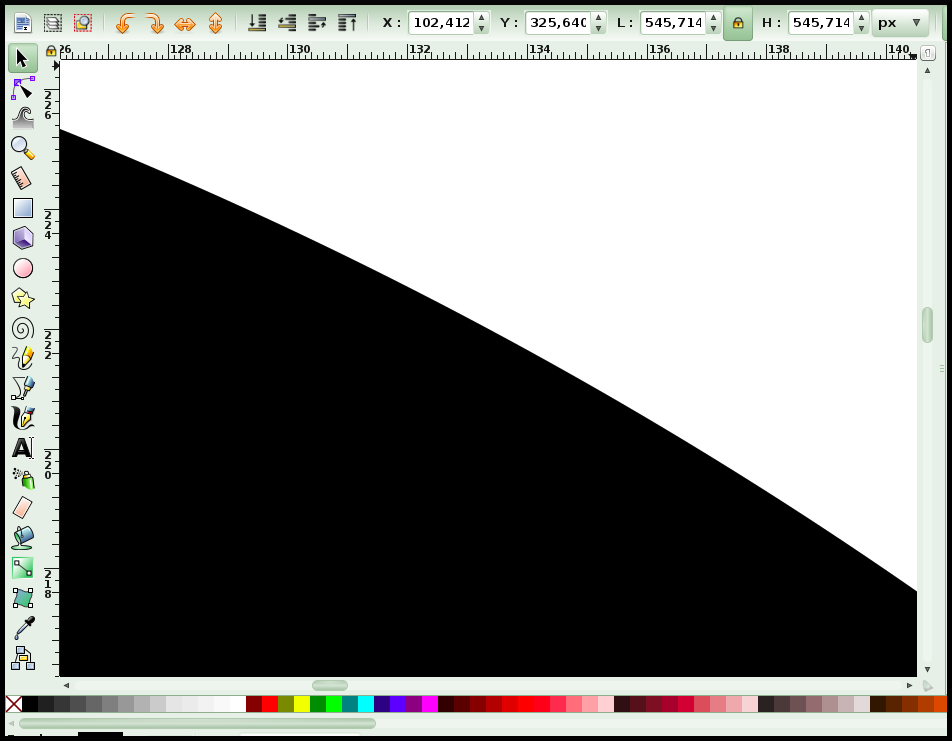
Je vais maintenant recommencer ma tambouille, mais cette fois-ci en dessinant un cercle sur Inkscape, qui, lui, permet de générer des images vectorielles. Voilà ce que nous obtenons en zoomant dessus :

Mazette ! Où sont donc passés mes pixels ? Eh bien ça dépend de ceux dont on parle. Les pixels de l’écran, eux, sont toujours là. Les pixels du fichier, par contre, ont disparu ! Pour la simple et bonne raison que nous sommes maintenant en présence d’un
fichier vectoriel, dont l’extension commune est .svg .

Nous utilisons ici une logique différente de stockage d’information. Pour schématiser, nous pourrions nous dire qu’au lieu de stocker directement l’image selon une suite de pixel, nous stockons une description de l’image, qui pourrait ressemblerait à ça :

Il s’agit d’instructions à dessiner, majoritairement composées de nombres, notamment de coordonnées relatives les unes aux autres, et de mots-clefs décrivant des formes graphiques, comme la courbe ou le rectangle.

Grâce à cette logique, le dessin n’est pas figé, mais nécessite une étape supplémentaire : il faut maintenant qu’il soit effectivement traduit en pixels afin de pouvoir être affiché à l’écran. Ainsi, le programme qui se charge de l’interpréter, dans notre cas Inkscape,
peut redessiner l’image à la bonne résolution indépendamment du zoom demandé. Il s’agit pour lui d’interpréter correctement les coordonnées contenues dans le fichier et de les adapter au zoom et à la résolution actuels.

Le vectoriel permet donc un redimensionnement infini. Cela vient du fait qu’au lieu de stocker des informations absolues, il ne contient que des relations entre les coordonnées, elles-même se référant à une valeur unique. En changeant cette valeur,
l’ensemble des relations est impactée et l’image entière est modifié aux bonnes proportions. De surcroît, ce système de coordonnées est également adapté à l’usinage, puisqu’il permet de fournir aux machines la position de leurs axes.

Vectoriel et matriciel : quels usages ?

On pourrait penser que la modularité du vectoriel relègue le matriciel au rang de technologie dépassée. Mais il n’en est rien. Comme vous vous en doutez, les deux formats sont en réalité complémentaires et n’ont pas vocation à être utilisés de la même manière.

En tout premier lieu, il n’est pas pertinent de prendre une « photo vectorielle ». Le monde n’étant pas constitué d’ellipses ou même de courbes, un tableau en deux dimensions contenant des couleurs correspond mieux à notre perception rétinienne, à condition que les pixels soient assez petits pour être indiscernables.

Cela implique que si nous souhaitons retoucher une photo, puis l’imprimer, le format matriciel paraît également plus approprié. À moins que la résolution de la photo soit ne trop basse, il ne semble pas nécessaire de changer son format lors de ces opérations. De surcroît, la vectorisation (le passage d’une image matricielle à une image vectorielle) modifie le rendu de celle-ci, et nous souhaitons en général garder le rendu originel.

Si nous souhaitons afficher une image à l’écran à différents niveaux de zoom, le vectoriel est plus approprié. Admettons que nous souhaitions faire une application interactive qui permette, depuis une image de la Terre vue de l’espace, de zoomer jusqu’à distinguer un brin d’herbe. Supposons qu’à taille maximale, ce brin d’herbe fasse 3 par 20 pixels, et que celui-ci est 10 000 fois plus petit que la Terre (ce qui est encore largement sous-estimé). Pour que le zoom sur le brin d’herbe respecte un ratio de 1 pixel dans le fichier pour 1 pixel à l’écran, il faudrait donc que la Terre, dans une image matricielle, fasse 200 000 pixels ! C’est beaucoup trop pour l’ordinateur. Or, en vectoriel, ce problème disparaît. L’écran calculera rapidement que le niveau de zoom est tel qu’il a juste à remplir l’écran de la couleur de la Terre, puis affichera le brin d’herbe au moment voulu. Bien sûr, c’est une exemple théorique, il existe de meilleures manières de concevoir un tel programme qu’un simple choix entre deux gigantesques fichiers.

Dans la même optique, le format vectoriel est très utilisé dans le web car il permet d’adapter automatiquement du contenu à la résolution du navigateur de l’utilisateur. Par ailleurs, nous n’avons parlé ici que d’un contenu gardant ses proportions, mais le vectoriel permet de déformer une image aisément, par exemple en élargissant un carré pour en faire un rectangle, ce que ne permet pas le matriciel, qui devrait ajouter ou supprimer des pixels arbitrairement.

De là suit que le vectoriel est préférable pour l’animation. Animer un dessin en images matricielles nécessite de dessiner chaque image l’une après l’autre. C’est un travail fastidieux et il est difficile d’obtenir une image fluide. Le vectoriel permet de bouger les points de référence de l’objet à animer ce qui simplifie la tâche. Les logiciels d’animation modernes, comme Krita, permettent même de ne configurer que des images clefs puis d’interpoler les positions des points entre ces images.